This is a guest post by Francisco Javier García Capitán on Generating equation with radicals 

RationalToString converts a number into a string. The number can be an integer or a fraction. It is used by ListToString.

RationalToString[num_]:=”x=” <>
If[Denominator[num]Š1,
ToString[num],
ToString[Numerator[num]]<>”/”<>ToString[Denominator[num]]]<>”, “

Examples :

RationalToString[4]
x=4,
RationalToString[5/2]
x=5/2,

ListToString converts a list of numbers into a string. It is used to show the solution(s) of an equation.

ListToString[lista_]:=StringDrop[Apply[StringJoin,Map[RationalToString,lista]],-2]<>”.”

Examples :

ListToString[{4}]
x=4.
ListToString[{4,5/2}]
x=4, x=5/2.

GenerateRadical[x0] returns a radical of the form  where √ax + b are choosen at random and having an integer value when x=x0. The idea is the generation of equation with integer solutions. We first generate the value total = a x0 + b, then we generate a and finally, b

GenerateRadical[x0_]:=Module [ { total,a,b},
total=RandomInteger[{1,5}];
a=RandomInteger[{1,5}];
b=total2-a x0;
]

Example: We use Table to get a list of eight radicals that have an integer value when x=5.

Table[GenerateRadical[5],{8}]

{ √-9+ 2x ,√ 5 √x ,√15+ 2 x ,√4+x ,√-4+4x ,√-6+3 x , √1+3 x ,√-4+x }

GenerateRadical[x0] returns an equation of the form c1  +c2 = d. We can specify a range for the values of the coefficients c1 and c2. We avoid the case c1=c2=0 by manually changing it to c1=1 c2=0.

GenerateEquation[x0_,rangocoefs_]:=Module[{c1, c2,rad1,rad2},
rad1=GenerateRadical[x0];
rad2=GenerateRadical[x0];
{c1, c2}=RandomInteger[rangocoefs,2];
If[And[c1Š0,c2Š0],c1=1];
c1 rad1 + c2 rad2 Š ((c1 rad1 + c2 rad2)/.x®x0)
]

Example :

GenerateEquation[2,{-3,3}]
-2 +2 Š0

SolvedEquation returns a pair {eqn, sols} formed by an equation and a string containing the solution(s) of the equation.

SolvedEquation[rangox_,rangocoefs_]:=Module[{x0,ecuacion,sols},
x0=RandomInteger[rangox];
ecuacion=GenerateEquation[x0,rangocoefs];
sols=x/.Solve[ecuacion,x];
{ecuacion,ListToString[sols]}
]

SolvedEquation[{-5,5},{-3,3}]
{+3 Š10,x=0.}

EquationList returns a numbered list of equations with their solutions.

EquationList[n_,rangox_,rangocoefs_]:=MapThread[Prepend,
{Table[SolvedEquation[rangox,rangocoefs],{n}],
Range[1,n]}] //TableForm

Off[Solve::ifun]
SolvedEquation

{

  1. {3√3+x +2√4+5x = Š12,     x=1.},
  2. {-√29+5x  = -Š-3,              x=-4.},
  3. {-2√-11+3x +Š√-16+5x,                          x=4.}

}

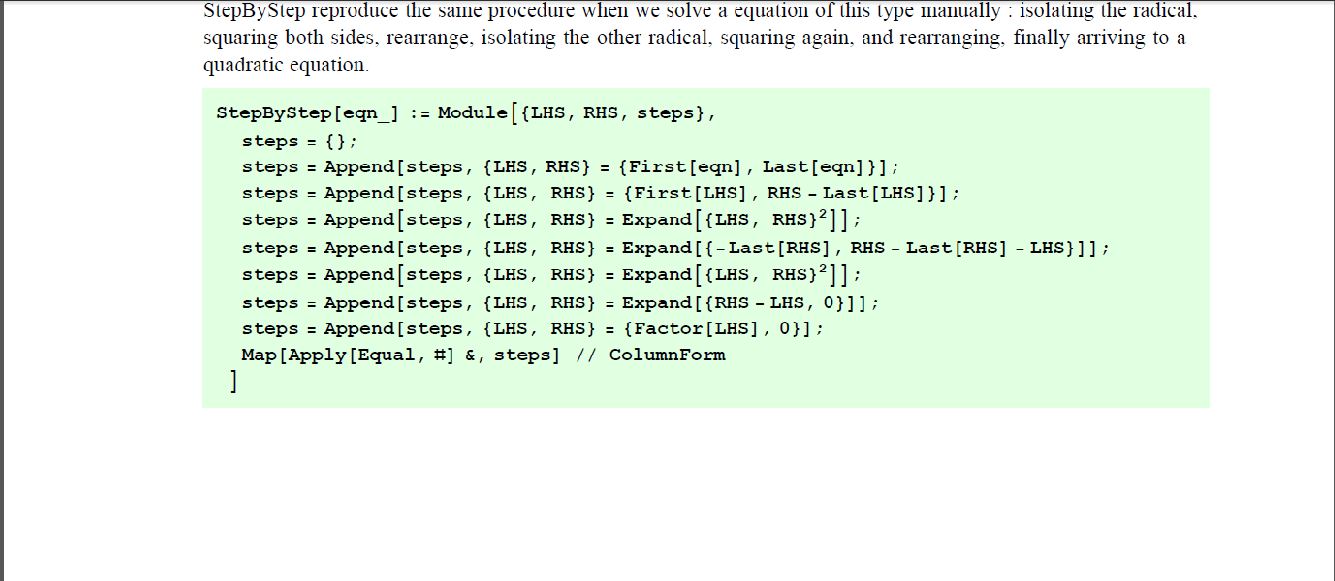
StepByStep reproduce the same procedure when we solve a equation of this type manually : isolating the radical, squaring both sides, rearrange, isolating the other radical, squaring again, and rearranging, finally arriving to a quadratic equation.

StepByStep[eqn_]:=Module[{LHS,RHS,steps},
steps={};
steps=Append[steps,{LHS,RHS}={First[eqn],Last[eqn]}];
steps=Append[steps,{LHS, RHS}={First[LHS],RHS-Last[LHS]}];
steps=Append[steps,{LHS, RHS}=Expand[{LHS, RHS}2]];
steps=Append[steps,{LHS, RHS}=Expand[{-Last[RHS],RHS-Last[RHS]-LHS}]];
steps=Append[steps,{LHS, RHS}=Expand[{LHS, RHS}2]];
steps=Append[steps,{LHS, RHS}=Expand[{RHS-LHS,0}]];
steps=Append[steps,{LHS, RHS}={Factor[LHS],0}];
Map[Apply[Equal,#]&,steps] // ColumnForm
]

StepByStep[√2+x -3√17+4x = Š-13]

√2+x -3√17+4x = -13
√2+x = -13 + 3√17+4x
2+x = 322 + 36x – 78√17+4x
78√17+4x 320 + 35x
103 428 + 24 336 x == 102 400 + 22 400 x  1225 x^2
-1028 – 1936 x + 1225 x^2 = 0
(-2+ x) (514 + 1225 x) = 0