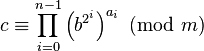Last digit problem in SPOJ looks simple but it contains a important concept of Modular exponentiation. If want AC in submission then you have to know about this concept ,to avoid time limit exceeded  .

For example, given b = 5, e = 3, and m = 13, the solution, c = 8, is the remainder of dividing 5^3 (125) by 13.

The general method is :

The most straightforward method of calculating a modular exponent is to calculate be directly, then to take this number modulo m. Consider trying to compute c, given b = 4, e = 13, and m = 497:

c \equiv 4^{13} \pmod{497}

One could use a calculator to compute 413; this comes out to 67,108,864. Taking this value modulo 497, the answer c is determined to be 445.

Note that b is only one digit in length and that e is only two digits in length, but the value be is 8 digits in length.

In strong cryptography, b is often at least 256 binary digits (77 decimal digits). Consider b = 5 × 1076 and e = 17, both of which are perfectly reasonable values. In this example, bis 77 digits in length and e is 2 digits in length, but the value be is 1,304 decimal digits in length.This leadto time limit exceeded.

Right-to-left binary method:

First convert e to it’s binary form:

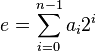e = \sum_{i=0}^{n-1} a_i 2^i , where  the length of e is n bits. ai can take the value 0 or 1 for any i such that 0 ≤ i < n – 1. By definition, an – 1 = 1.

So now solution is :

b^e = b^{\left( \sum_{i=0}^{n-1} a_i 2^i \right)} = \prod_{i=0}^{n-1} \left( b^{2^i} \right) ^ {a_i}

The solution c is therefore:

c \equiv \prod_{i=0}^{n-1} \left( b^{2^i} \right) ^ {a_i}\ (\mbox{mod}\ m)

Now how will be your program approach :

while exponent > 0
        if (exponent mod 2 == 1):
           result := (result * base) mod modulus
        exponent := exponent >> 1
        base := (base * base) mod modulus
    return result

So the function will be like this :

void lastdig{
 scanf("%lld%lld",&n1,&n2);
 long long d=1;
 while(n2){
      if(n2%2 !=0)//it can be 0 or 1
             {
             d=(d*n1)%10; 
             }
     n2 >>=1;
    n1=(n1*n1)%10;
        }
 printf("%lld\n",d);
 }

Hope you learnt something #HappyCoding. 🙂
Source : wikipedia.org